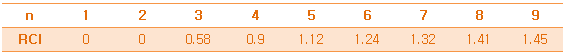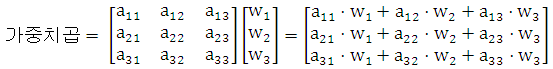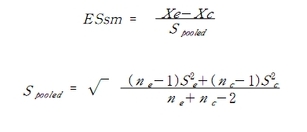출처 : http://blog.naver.com/kwanseol?Redirect=Log&logNo=20057518639
요인분석(factor analysis)란?
요인분석이란 말 그래도 어떤 변수들간의 잠재요인(latent factor)가 있어 개별 변수들을
설명하고 있음을 통계적으로 도출하는 분석을 의미한다.
좀더 쉽게 예를 들어 설명하면,
사람들에 대한 인사평가를 한다고 생각해보자, 학력, 영어점수, 자격증, 대인관계, 과거 직장경력 등 다양한 부분에 대한 평가결과가 있다고 한다면 이와 같은 변수들에 대한 평가가 잠재력, 조직관리력 등 어떤 요인(factor)들이 있고 이것이 학력, 영어점수, 자격증 등의 평가점수에 투명되어 나타난다는 것이다. 그래서 학술적 논점으로 그와 같은 요인(factor)를 찾아내는 과정을 요인분석의 대체적 흐름이다.
보자 직접적으로 설명하면, 개별 변수간의 상관관계(즉 거리 distance, 거리가 가깝다는 것은 상관관계가 높다는 것임)를 가지고 상관관계가 높은 변수들끼리 묶고 이들을 어떤 요인(factor)의 함수식으로 표현하는 것이다. 사실 주성분분석과 동일한 개념이라고 볼 수 있다. 다만, 주성분이 변수들을 대표한다면 요인은 변수들을 설명한다고 볼 수 있다. 즉 주성분 = f(변수) 라면 변수 = f(요인)으로 이해하면 쉽겠다.
여기서 요인과 변수의 관계에 대한 사전지식이 없는 것을 탐색적 요인분석(explorative)이라고 하고
확증적요인분석(comfirmative)의 경우 소위 말해서 경로분석(path analysis)라고 한다. 사실 확증적 요인분석은 이미 가설에 의해 개별 변수들간에 방향성과 상관성이 이론적으로 주워지고 이를
통계적으로 입증하는 분석방법이다.
추후에 경로분석에 대해 설명할 기회가 있겠지?. 시간나면 정리해 보겠습니다.
그럼 어떻게 진행하느냐이다.
설문조사 등을 통해 여러 문항의 결과 즉 x1,x2,x3... x100이 있다고 하자.
이와 같은 변수들을 요인분석을 통해 도출해 보면
우선 잠재된 요인들을 어느 수준에서 도출된다, 예를 들어 f1, f2, f3, f4로 도출된다.
이들 f1, f2, f3, f4들은 서로 상관관계가 없는 독립된 새로운 요인으로 등장하게 된다
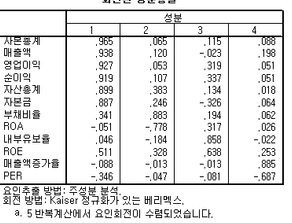
예를들어 위의 경우와 같이 f1은 자본총계, 매출액 등 "규모"의 요인으로 볼 수 있고
f2는 부채비율 등 "건전성" 요인으로 볼 수 있겠다.
통상 이와 같은 요인은 회전(rotation) 즉 회전방법에 따라 요인부하치(factor loading value)가
달라지는데, varimax, promax 등의 회전법이 주로 사용된다.
사실 연구자나 분석하는 사람의 성향에 따라 회전방법은 선택할 수 있으며 개별 요인들이
직교 즉 로딩값들이 (+), (-)가 나오는 회전방법이 추천하는 방법이다.
그러면 어디에 활용되나?
바로 이부분이다. 이와 같이 요인이 나오면 개별 관측치들은 요인점수가 나온다. 즉 개별변수들에 미치는 로딩값들을 통해 개별 관측치(observation)의 f1 요인값, f2 요인값 들이 나오게 된다.
다른 표현으로 하면 개별 관측치들의 "규모"값, "건전성"값들이 나오고 이를 가지고
추가적인 회귀분석, GLM분석등을 실시할 수 있다는 것이다.
또한, 수많은 변수(X1, X2, X3 ... X100) 등을 간단히 몇개의 요인(factor)로 집약하여
축약된 그리고 개념화된 변수 혹은 요인으로 "설명"한다는 것이다.
우리의 인지구조상 잠재된 요인이 있고 이것이 몇몇 변수들로 형상화되고 있음을
입증할 수 있다는 것이다.
예를 들어, 사람에 대한 평가를 여러 설문문항 100개의 문항으로 평가를 하고 나서
이에 대한 요인분석을 하면, 인물, 능력 등으로 요인이 도출된다면
우리가 사람에 대한 평가를 인물, 능력 등의 차원에서 이루어지고 있음을 입증할 수 있다는
말이다.
'분석기법' 카테고리의 다른 글
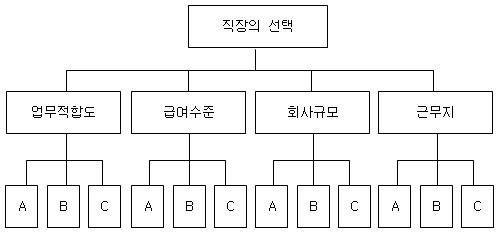
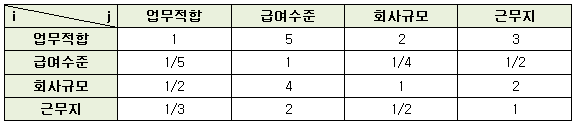
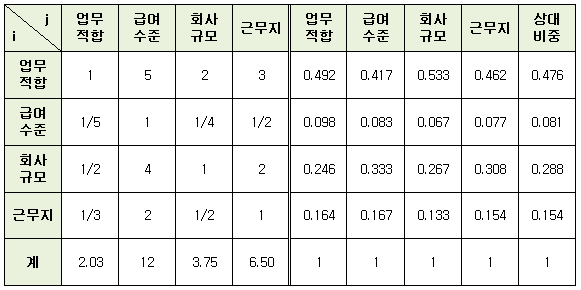
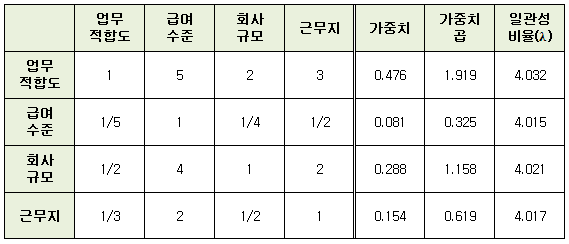
| [펀글] AHP(Analytic Hierarchy Process) (0) | 2011.12.14 |
|---|---|
| [펀글] 메타분석(meta analysis) (0) | 2011.12.14 |